布隆过滤器

什么是布隆过滤器

布隆过滤器（Bloom Filter），是1970年由布隆提出的。它是由一个很长的二进制向量和一系列映射函数组成。本质上布隆过滤器是一种数据结构，比较巧妙的概率型数据结构（probabilistic data structure），特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”。

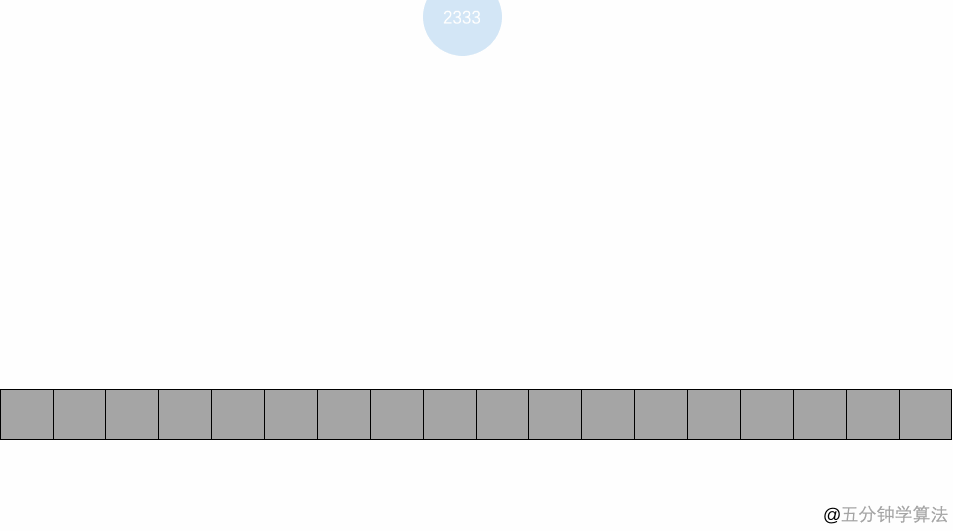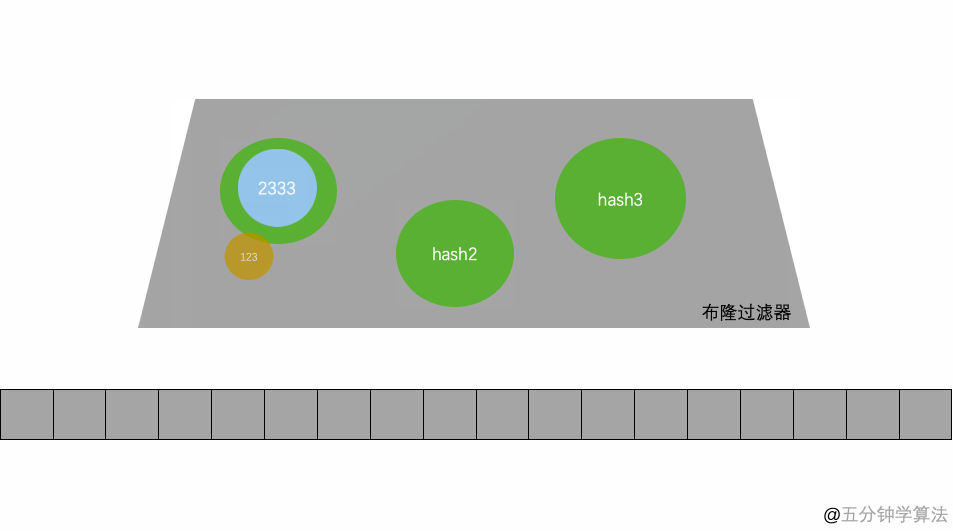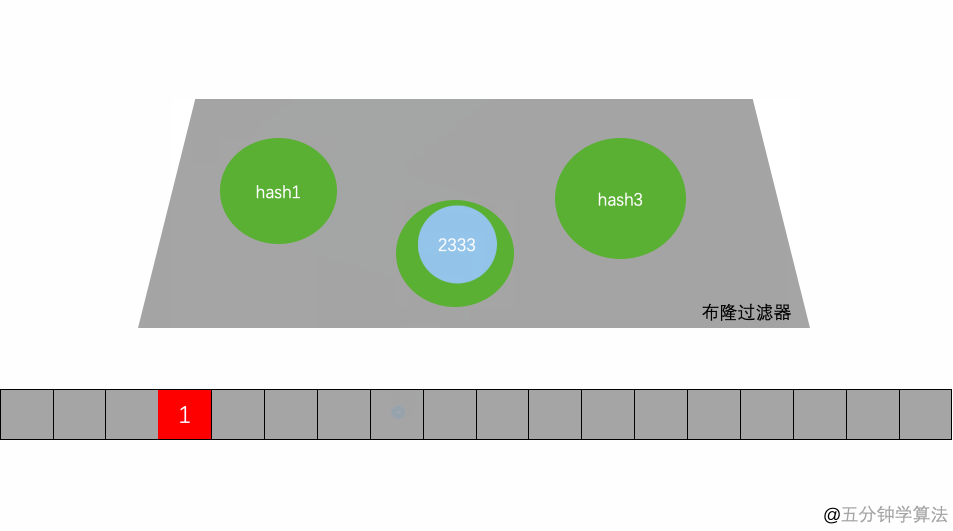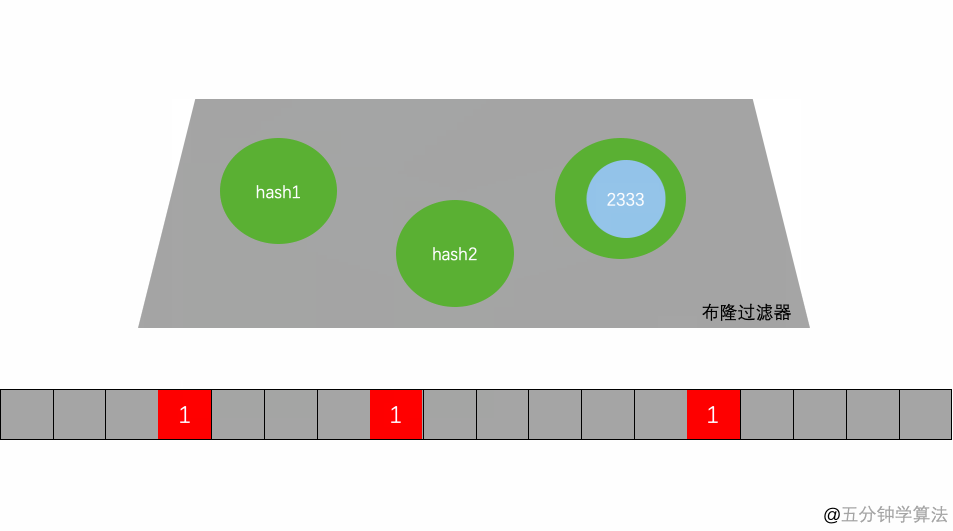
图中的，映射函数就是hash1(),hash2(),hash3()就是映射函数。下面的存放的就是一个超长二进制向量。一个数通过三次计算，映射到三个不同的地方。这个就是存储过程。

还有一个就是判断，就是根据过来的值，再去hash三次，看是否能在二进制向量上找到存在的值。如果三次都是1，说明这个值可能存在，反之是一定不存在。也就是说布隆过滤器上，如果存在（不一定真的存在，可能是冲突）。如果不存在那就一定不存在。所以一般使用都是通过这一个不存在的这个特性去处理。用英语说：False is always false. True is maybe true。

相比于传统的 List，Tree，Map 等数据结构，它更高效、占用空间更少，但是缺点是其返回的结果是概率性的，而不是确切的。

为什么要用布隆过滤器

举个栗子：一个网站有 100 亿 url 存在一个黑名单中，每条 url 平均 64 字节。这个黑名单要怎么存？若此时随便输入一个 url，你如何快速判断该 url 是否在这个黑名单中

如果想判断一个元素是不是在一个集合里，一般想到的是将集合中所有元素保存起来，然后通过比较确定。 List，Tree，Map等等数据结构都是这种思路。但是随着集合中元素的增加，我们需要的存储空间越来越大。同时检索速度也越来越慢，上述三种结构的检索时间复杂度分别为O(n),O($logn$),O(1)。

100 亿是一个很大的数量级，这里每条 url 平均 64 字节，全部存储的话需要 640G 的内存空间。又因为使用了散列表这种数据结构，而散列表是会出现散列冲突的。为了让散列表维持较小的装载因子，避免出现过多的散列冲突，需要使用链表法来处理，这里就要存储链表指针。因此最后的内存空间可能超过 1000G 了。明显我们是不能采用这种方法。

我们就不能把这些东西全都存储到内存中，而是通过映射，然后只生成一个二进制向量。不过对于100亿这个数据量比较大，可能初始化的时间会比较长，如果不经常变动的化，我们可以讲创建好的二进制向量持久化。不用每次动态计算。

所以说布隆过滤器是一个占用空间特别小的，而且特别高效的一种数据结构。我们一般使用它处理大量数据的集合。

布隆过滤器的特性

通过上面我们知道布隆过滤器会有误报。如果布隆过滤器的大小太小，很快就会将所有位字段变为“1”，然后我们的布隆过滤器将为每个输入返回“误报”。因此，布隆过滤器的大小是一个非常重要的决定。较大的过滤器将具有较少的误报，并且较小的一个。因此，我们可以根据“误报误差率”调整我们的布隆过滤器以确定我们需要多少精确度。

另一个重要参数是“我们将使用多少哈希函数”。我们使用的哈希函数越多，布隆过滤器就越慢，填充越快二进制长度和hash函数个数，如果hash函数过多那么查找就会慢下来，怎么才能最合适，实现比较小的误报和最小存储。

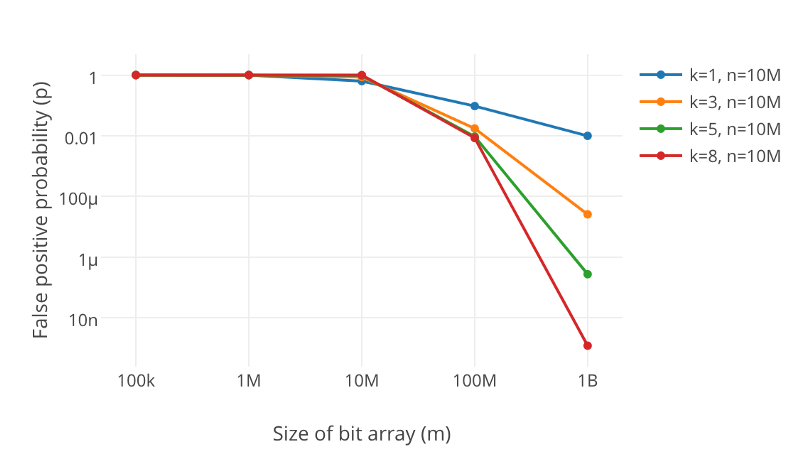
图中数据量是N=10M，纵坐标是表示误报率，横坐标是二进制向量大小。K是函数个数

我们可以根据过滤的大小，m，散列函数的数量，k和插入的元素数n来计算误差率p，公式如下：

$p=(1-e^{-k*n/m})^k$

如果p确定的话，我们就可以导出，K和M的大小，当N数量值一定的时候。

$m={-n*lnp}/{(ln2)^2}$ $K=(m/n)*ln2$

上面说道布隆过滤器也可能会误报，一般我们都是逻辑反向使用布隆过滤器。如果你要正向使用也可以，常见的补救办法是在建立一个小的白名单，存储那些可能别误判值。这个也是常见过滤可疑邮件。

还有一个点，就是布隆过滤器是不支持删除，因为，在二进制向量中，一个bit位会被多个值删除，如果删除一个bit位那么会产生多个值，找不到。

布隆过滤器的使用和java自己实现

我们一般没必要自己去写一个过滤器，在google 的guava的包中，有布隆过滤器的实现，我们可以拿过就用。

package com.qjq.guava;

import com.google.common.base.Charsets;
import com.google.common.base.Joiner;
import com.google.common.base.Splitter;
import com.google.common.collect.Lists;
import com.google.common.hash.BloomFilter;
import com.google.common.hash.Funnel;
import com.google.common.hash.Sink;

import java.util.List;

public class GuavaTestClient {
    public static void main(String[] args) {
    // 1. 创建符合条件的布隆过滤器
        BloomFilter<String> filter = BloomFilter.create(new Funnel<String>() {
            @Override
            public void funnel(String from, Sink into) {
                into.putString(from, Charsets.UTF_8);
            }
        }, 10000, 0.0001);
     //2. 将一部分数据添加进去
        for (int index = 0; index < 6000; index++) {
            filter.put("abc_test_" + index);
        }
        System.out.println("write all...");
       // 3. 测试结果
        for (int i = 5000; i < 10000; i++) {
            if (filter.mightContain("abc_test_" + i)) {
                System.out.println("yes：" + i);
            }
        }
    }
}
//会打印1000个yes从5000-5999。这个只是demo

如果你要自己实现也可以。

package com.qjq.guava.filter;

import java.util.BitSet;

public class BloomTest {

    public static void main(String[] args) {
		//向布隆过滤器中添加值
        BloomFilter b = new BloomFilter();
        b.addValue("www.baidu.com");
        b.addValue("www.sohu.com");
		//判断是否存在
        System.out.println(b.contains("www.baidu.com"));
        System.out.println(b.contains("www.sina.com"));
    }
}

class BloomFilter {

    private static final int BIT_SIZE = 2 << 28;//二进制向量的位数，相当于能存储1000万条url左右，误报率为千万分之一
    private static final int[] seeds = new int[]{3, 5, 7, 11, 13, 31, 37, 61};//用于生成信息指纹的8个随机数，最好选取质数。hash8次生成8个位置在二进制向量

    private BitSet bits = new BitSet(BIT_SIZE);//二进制向量大小
    private Hash[] func = new Hash[seeds.length];//用于存储8个随机哈希值对象

    public BloomFilter() {//构造的时候生成hash种子，对hash存储对象。
        for (int i = 0; i < seeds.length; i++) {
            func[i] = new Hash(BIT_SIZE, seeds[i]);
        }
    }

    /**
     * 像过滤器中添加字符串
     */
    public void addValue(String value) {
        //将字符串value哈希为8个或多个整数，然后在这些整数的bit上变为1
        if (value != null) {
            for (Hash f : func)
                bits.set(f.hash(value), true);
        }

    }

    /**
     * 判断字符串是否包含在布隆过滤器中
     */
    public boolean contains(String value) {
        if (value == null)
            return false;

        boolean ret = true;

        //将要比较的字符串重新以上述方法计算hash值，再与布隆过滤器比对
        for (Hash f : func)
            ret = ret && bits.get(f.hash(value));
        return ret;
    }

    /**
     * 随机哈希值对象
     */

    public static class Hash {
        private int size;//二进制向量数组大小
        private int seed;//随机数种子

        public Hash(int cap, int seed) {
            this.size = cap;
            this.seed = seed;
        }

        /**
         * 计算哈希值(也可以选用别的恰当的哈希函数)，也就是二进制向量计算位置
         */
        public int hash(String value) {
            int result = 0;
            int len = value.length();
            for (int i = 0; i < len; i++) {
                result = seed * result + value.charAt(i);
            }

            return (size - 1) & result;
        }
    }

}

总结

布隆过滤器的常见实践

网页爬虫对URL的去重，避免爬取相同的URL地址；

反垃圾邮件，从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱（同理，垃圾短信）

缓存击穿，将已存在的缓存放到布隆中，当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。

都是利用bloom-filter 的高效和占用空间小。而且这种对误判没有那么搞的要求，就算误判一次或者几次，不会有无法弥补的损失。

布隆过滤器的优点

相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数O(k)。另外, 散列函数相互之间没有关系，方便由硬件并行实现。布隆过滤器不需要存储元素本身，在某些对保密要求非常严格的场合有优势。

布隆过滤器可以表示全集，其它任何数据结构都不能；

k和m相同，使用同一组散列函数的两个布隆过滤器的交并差运算可以使用位操作进行

布隆过滤器的缺点

但是布隆过滤器的缺点和优点一样明显。误算率是其中之一。随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣。

另外，一般情况下不能从布隆过滤器中删除元素. 我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。

在降低误算率方面，有不少工作，使得出现了很多布隆过滤器的变种。